In mathematics and in particular in combinatorics, the Lehmer code is a particular way to encode each possible permutation of a sequence of n numbers. It is an instance of a scheme for numbering permutations and is an example of an inversion table.
The code
The Lehmer code makes evident the fact that there are
permutations of a sequence of n numbers. If a permutation σ is specified by the sequence (σ1, …, σn) of its images of 1, …, n, then it is encoded by a sequence of n
numbers, but not all such sequences are valid since every number must
be used only once. By contrast the encodings considered here choose the
first number from a set of n values, the next number from a fixed set of n − 1
values, and so forth decreasing the number of possibilities until the
last number for which only a single fixed value is allowed; every sequence of numbers chosen from these sets encodes a single permutation. While several encodings can be defined, the Lehmer code has several additional useful properties; it is the sequence
in other words the term L(σ)i counts the number of terms in (σ1, …, σn) to the right of σi that are smaller than it, a number between 0 and n − i, allowing for n + 1 − i different values.
A pair of indices (i,j) with i < j and σi > σj is called an inversion of σ, and L(σ)i counts the number of inversions (i,j) with i fixed and varying j. It follows that L(σ)1 + L(σ)2 + … + L(σ)n is the total number of inversions of σ,
which is also the number of adjacent transpositions that are needed to
transform the permutation into the identity permutation. Other
properties of the Lehmer code include that the lexicographical order of the encodings of two permutations is the same as that of their sequences (σ1, …, σn), that any value 0 in the code represents a right-to-left minimum in the permutation (i.e., a σi smaller than any σj to its right), and a value n − i at position i similarly signifies a right-to-left maximum, and that the Lehmer code of σ coincides with the factorial number system representation of its position in the list of permutations of n in lexicographical order (numbering the positions starting from 0).
Variations of this encoding can be obtained by counting inversions (i,j) for fixed j rather than fixed i, by counting inversions with a fixed smaller value σj rather than smaller index i,
or by counting non-inversions rather than inversions; while this does
not produce a fundamentally different type of encoding, some properties
of the encoding will change correspondingly. In particular counting
inversions with a fixed smaller value σj gives the inversion table of σ, which can be seen to be the Lehmer code of the inverse permutation.
Encoding and decoding
The usual way to prove that there are n! different permutations of n objects is to observe that the first object can be chosen in n different ways, the next object in n − 1 different ways (because choosing the same number as the first is forbidden), the next in n − 2
different ways (because there are now 2 forbidden values), and so
forth. Translating this freedom of choice at each step into a number,
one obtains an encoding algorithm, one that finds the Lehmer code of a
given permutation. One need not suppose the objects permuted to be
numbers, but one needs a total ordering of the set of objects. Since the code numbers are to start from 0, the appropriate number to encode each object σi by is the number of objects that were available at that point (so they do not occur before position i), but which are smaller than the object σi actually chosen. (Inevitably such objects must appear at some position j > i, and (i,j) will be an inversion, which shows that this number is indeed L(σ)i.)
This number to encode each object can be found by direct counting, in
several ways (directly counting inversions, or correcting the total
number of objects smaller than a given one, which is its sequence number
starting from 0 in the set, by those that are unavailable at its
position). Another method which is in-place, but not really more
efficient, is to start with the permutation of {0, 1, … n − 1} obtained by representing each object by its mentioned sequence number, and then for each entry x, in order from left to right, correct the items to its right by subtracting 1 from all entries (still) greater than x (to reflect the fact that the object corresponding to x
is no longer available). Concretely a Lehmer code for the permutation
B,F,A,G,D,E,C of letters, ordered alphabetically, would first give the
list of sequence numbers 1,5,0,6,3,4,2, which is successively
transformed
where the final line is the Lehmer code (at each line one subtracts 1
from the larger entries to the right of the boldface element to form
the next line).
For decoding a Lehmer code into a permutation of a given set, the latter procedure may be reversed: for each entry x, in order from right to left, correct the items to its right by adding 1 to all those (currently) greater than or equal to x; finally interpret the resulting permutation of {0, 1, … n − 1} as sequence numbers (which amounts to adding 1 to each entry if a permutation of {1, 2, … n}
is sought). Alternatively the entries of the Lehmer code can be
processed from left to right, and interpreted as a number determining
the next choice of an element as indicated above; this requires
maintaining a list of available elements, from which each chosen element
is removed. In the example this would mean choosing element 1 from
{A,B,C,D,E,F,G} (which is B) then element 4 from {A,C,D,E,F,G} (which is
F), then element 0 from {A,C,D,E,G} (giving A) and so on,
reconstructing the sequence B,F,A,G,D,E,C.
Applications to combinatorics and probabilities
Independence of relative ranks
The Lehmer code defines a bijection from the symmetric group Sn to the Cartesian product ![[n]\times[n-1]\times\cdots\times[2]\times[1]](http://upload.wikimedia.org/math/2/8/d/28d0b899fce0d4fb84c8b7ee36b1ba69.png) , where [k] designates the k-element set
, where [k] designates the k-element set 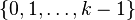 . As a consequence, under the uniform law on the Sn, the component L(σ)i defines a uniformly distributed random variable on [n + 1 − i], and these random variables are mutually independent, because they are projections on different factors of a Cartesian product.
. As a consequence, under the uniform law on the Sn, the component L(σ)i defines a uniformly distributed random variable on [n + 1 − i], and these random variables are mutually independent, because they are projections on different factors of a Cartesian product.
![[n]\times[n-1]\times\cdots\times[2]\times[1]](http://upload.wikimedia.org/math/2/8/d/28d0b899fce0d4fb84c8b7ee36b1ba69.png) , where [k] designates the k-element set
, where [k] designates the k-element set 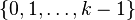 . As a consequence, under the uniform law on the Sn, the component L(σ)i defines a uniformly distributed random variable on [n + 1 − i], and these random variables are mutually independent, because they are projections on different factors of a Cartesian product.
. As a consequence, under the uniform law on the Sn, the component L(σ)i defines a uniformly distributed random variable on [n + 1 − i], and these random variables are mutually independent, because they are projections on different factors of a Cartesian product.Number of right-to-left minima and maxima
Definition : In a sequence u=(uk)1≤k≤n, there is right-to-left minimum (resp. maximum) at rank k if uk is strictly smaller (resp. strictly bigger) than each element ui with i>k, i.e., to its right.
Let B(k) (resp. H(k)) be the event "there is right-to-left minimum (resp. maximum) at rank k", i.e. B(k) is the set of the permutations  which exhibit a right-to-left minimum (resp. maximum) at rank k. We clearly have
which exhibit a right-to-left minimum (resp. maximum) at rank k. We clearly have
 which exhibit a right-to-left minimum (resp. maximum) at rank k. We clearly have
which exhibit a right-to-left minimum (resp. maximum) at rank k. We clearly have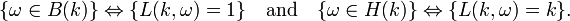
Thus the number Nb(ω) (resp. Nh(ω)) of right-to-left minimum (resp. maximum) for the permutation ω can be written as a sum of independent Bernoulli random variables each with a respective parameter of 1/k :

Indeed, as L(k) follows the uniform law on ![\scriptstyle\ [\![1,k]\!],\](http://upload.wikimedia.org/math/a/0/5/a053d4521db1b9f4355f4114bc620fc6.png)
![\scriptstyle\ [\![1,k]\!],\](http://upload.wikimedia.org/math/a/0/5/a053d4521db1b9f4355f4114bc620fc6.png)

The generating function for the Bernoulli random variable  is
is
 is
is
therefore the generating function of Nb is

which allow us to find again the product form for the generative series of the Stirling numbers of the first kind (unsigned).
The secretary problem
This is an optimal stop problem, a classic in decision theory,
statistics and applied probabilities, where a random permutation is
gradually revealed through the first elements of its Lehmer code, and
where the goal is to stop exactly at the element k such as σ(k)=n,
whereas the only available information (the k first values of the Lehmer
code) is not sufficient to compute σ(k).
In less mathematical words : a series of n applicants are interviewed
one after the other. The interviewer must hire the best applicant, but
must make his decision (“Hire” or “Not hire”) on the spot, without
interviewing the next applicant ( and a fortiori without interviewing all applicants).
The interviewer thus knows the rank of the kth applicant, therefore, at the moment of making his kth
decision, the interviewer knows only the k first elements of the Lehmer
code whereas he would need to know all of them to make a well informed
decision. To determine the optimal strategies (i.e. the strategy
maximizing the probability of a win), the statistical properties of the
Lehmer code are crucial.
Allegedly, Johannes Kepler clearly exposed this secretary problem
to a friend of his at a time when he was trying to make up his mind and
choose one out eleven prospective brides as his second wife. His first
marriage had been an unhappy one, having been arranged without himself
being consulted, and he was thus very concerned that he could reach the
right decision.



Tidak ada komentar:
Posting Komentar