In combinatorics, the factorial number system, also called factoradic, is a mixed radix numeral system adapted to numbering permutations. It is also called factorial base, although factorials do not function as base, but as place value of digits. By converting a number less than n! to factorial representation, one obtains a sequence of n digits that can be converted to a permutation of n in a straightforward way, either using them as Lehmer code or as inversion table representation; in the former case the resulting map from integers to permutations of n lists them in lexicographical order. General mixed radix systems were studied by Georg Cantor. The term "factorial number system" is used by Knuth, while the French equivalent "numération factorielle" was first used in 1888. The term "factoradic", which is a portmanteau of factorial and mixed radix, appears to be of more recent date.
Definition
The factorial number system is a mixed radix numeral system: the i-th digit from the right has base i, which means that the digit must be strictly less than i, and that (taking into account the bases of the less significant digits) its value to be multiplied by (i − 1)! (its place value).
| Radix | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Place value | 7! | 6! | 5! | 4! | 3! | 2! | 1! | 0! |
| Place value in decimal | 5040 | 720 | 120 | 24 | 6 | 2 | 1 | 1 |
| Highest digit allowed | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
From this it follows that the rightmost digit is always 0, the second
can be 0 or 1, the third 0, 1 or 2, and so on. The factorial number
system is sometimes defined with the 0! place omitted because it is
always zero (sequence A007623 in OEIS). Conversely, a further unchanging zero digit may be added in the rightmost position for the 0! place.
In this article, a factorial number representation will be flagged by a subscript "!", so for instance 341010! stands for 364514031201, whose value is
- =3×5! + 4×4! + 1×3! + 0×2! + 1×1! + 0×0!
- =((((3×5 + 4)×4 + 1)×3 + 0)×2 + 1)×1 + 0
- = 46310.
(Note that the place value is one less than the radix position, which is why these equations begin with 5!.)
General properties of mixed radix number systems also apply to the
factorial number system. For instance, one can convert a number into
factorial representation producing digits from right to left, by
repeatedly dividing the number by the place values (1, 2, 3, ...),
taking the remainder as digits, and continuing with the integer quotient, until this quotient becomes 0.
For example, 46310 can be transformed into a factorial representation by these successive divisions.
- 463 ÷ 5! = 3 with a remainder of 103
- 103 ÷ 4! = 4 and remainder 7
- 7 ÷ 3! = 1 and remainder 1
- 1 ÷ 2! = 0 and remainder 1
- 1 ÷ 1! = 1 and remainder 0
- 0 ÷ 0! = 0 and remainder 0
In principle, this system may be extended to represent fractional
numbers, though rather than the natural extension of place values (−1)!,
(−2)!, etc., which are undefined, the symmetric choice of radix values n
= 0, 1, 2, 3, 4, etc. after the point may be used instead. Again, the 0
and 1 places may be omitted as these are always zero. The corresponding
place values are therefore 1/1, 1/1, 1/2, 1/6, 1/24, ..., 1/n!, etc.
Examples
Here are the first twenty-four numbers, counting from zero.
The table on the left shows permutations, and inversion vectors
(which are reflected factorial numbers) below them. Another column
shows the inversion sets. The digit sums of the inversion vectors (or
factorial numbers) and the cardinalities of the inversion sets are equal
(and have the same parity as the permutation). They form the sequence  A034968.
A034968.

showing permutations and their inversion vectors
(compare version with factorial numbers)
The arrows indicate the bitwise less or equal
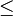 relation.
relation. |
|
For another example, the greatest number that could be represented with six digits would be 543210! which equals 719 in decimal:
- 5×5! + 4×4! + 3x3! + 2×2! + 1×1! + 0×0!.
Clearly the next factorial number representation after 543210! is 1000000! which designates 6! = 72010, the place value for the radix-7 digit. So the former number, and its summed out expression above, is equal to:
- 6! − 1.
The factorial number system provides a unique representation for each
natural number, with the given restriction on the "digits" used. No
number can be represented in more than one way because the sum of
consecutive factorials multiplied by their index is always the next
factorial minus one:
This can be easily proved with mathematical induction.
However, when using Arabic numerals
to write the digits (and not including the subscripts as in the above
examples), their simple concatenation becomes ambiguous for numbers
having a "digit" greater than 9. The smallest such example is the number
10 × 10! = 3628800010, which may be written A0000000000!, but not 100000000000! which denotes 11!=3991680010.
Thus using letters A–Z to denote digits 10, ..., 35 as in other base-N
make the largest representable number
36! − 1=37199332678990121746799944815083519999999910. For
arbitrarily greater numbers one has to choose a base for representing
individual digits, say decimal, and provide a separating mark between
them (for instance by subscripting each digit by its base, also given in
decimal). In fact the factorial number system itself is not truly a numeral system in the sense of providing a representation for all natural numbers using only a finite alphabet of symbols.
Permutations
There is a natural mapping between the integers 0, ..., n! − 1 (or equivalently the numbers with n digits in factorial representation) and permutations of n elements in lexicographical order, when the integers are expressed in factoradic form. This mapping has been termed the Lehmer code (or inversion table). For example, with n = 3, such a mapping is
| decimal | factorial | permutation |
| 010 | 000! | (0,1,2) |
| 110 | 010! | (0,2,1) |
| 210 | 100! | (1,0,2) |
| 310 | 110! | (1,2,0) |
| 410 | 200! | (2,0,1) |
| 510 | 210! | (2,1,0) |
The leftmost factoradic digit 0, 1, or 2 is chosen as the first
permutation digit from the ordered list (0,1,2) and is removed from the
list. Think of this new list as zero indexed and each successive digit
dictates which of the remaining elements is to be chosen. If the second
factoradic digit is "0" then the first element of the list is selected
for the second permutation digit and is then removed from the list.
Similarly if the second factoradic digit is "1", the second is selected
and then removed. The final factoradic digit is always "0", and since
the list now contains only one element it is selected as the last
permutation digit.
The process may become clearer with a longer example. For example, here is how the digits in the factoradic 4041000! (equal to 298210) pick out the digits in (4,0,6,2,1,3,5), the 2982nd permutation of the numbers 0 through 6.
4041000! → (4,0,6,2,1,3,5)
factoradic: 4 0 4 1 0 0 0!
| | | | | | |
(0,1,2,3,4,5,6) -> (0,1,2,3,5,6) -> (1,2,3,5,6) -> (1,2,3,5) -> (1,3,5) -> (3,5) -> (5)
| | | | | | |
permutation:(4, 0, 6, 2, 1, 3, 5)
A natural index for the group direct product of two permutation groups is the concatenation of two factoradic numbers, with two subscript "!"s.
concatenated
decimal factoradics permutation pair
010 000!000! ((0,1,2),(0,1,2))
110 000!010! ((0,1,2),(0,2,1))
...
510 000!210! ((0,1,2),(2,1,0))
610 010!000! ((0,2,1),(0,1,2))
710 010!010! ((0,2,1),(0,2,1))
...
2210 110!200! ((1,2,0),(2,0,1))
...
3410 210!200! ((2,1,0),(2,0,1))
3510 210!210! ((2,1,0),(2,1,0))
Fractional values
Unlike single radix systems whose place values are basen
for both positive and negative integral n, the factorial number base
cannot be extended to negative place values as these would be (−1)!,
(−2)! and so on, and these values are undefined.
One possible extension is therefore to use 1/0!, 1/1!, 1/2!, 1/3!,
..., 1/n! etc. instead, possibly omitting the 1/0! and 1/1! places which
are always zero.
With this method, all rational numbers have a terminating expansion,
whose length in 'digits' is less than or equal to the denominator of the
rational number represented. This may be proven by considering that
there exists a factorial for any integer and therefore the denominator
divides into its own factorial even if it does not divide into any
smaller factorial.
By necessity, therefore, the factoradic expansion of the reciprocal
of a prime has a length of exactly that prime (less one if the 1/1!
place is omitted). It can also be proven that the last 'digit' or term
of the representation of a rational with prime denominator is equal to
the difference between the numerator and the prime denominator.
There is also a non-terminating equivalent for every rational number
akin to the fact that in decimal 0.24999... = 0.25 = 1/4 and 0.999... = 1,
etc., which can be created by reducing the final term by 1 and then
filling in the remaining infinite number of terms with the highest value
possible for the radix of that position.
In the following selection of examples, spaces are used to separate
the place values, otherwise represented in decimal, and the places whose
values are always zero (1!, 0!, 1/1!) have been omitted. The rational
numbers on the left are also in decimal:
There are also a small number of constants have patterned representations with this method:













Tidak ada komentar:
Posting Komentar