Decimal Notation

Decimal notation is the writing of numbers in a base-10 numeral system. Examples are Roman numerals, Brahmi numerals, and Chinese numerals, as well as the Hindu-Arabic numerals used by speakers of many European languages. Roman numerals have symbols for the decimal powers (1, 10, 100, 1000) and secondary symbols for half these values (5, 50, 500). Brahmi numerals have symbols for the nine numbers 1–9, the nine decades 10–90, plus a symbol for 100 and another for 1000. Chinese numerals have symbols for 1–9, and additional symbols for powers of 10, which in modern usage reach 10⁴⁴.

However, when people who use Hindu-Arabic numerals speak of decimal notation, they often mean not just decimal numeration, as above, but also decimal fractions, all conveyed as part of a positional system. Positional decimal systems include a zero and use symbols (called digits) for the ten values (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) to represent any number, no matter how large or how small. These digits are often used with a decimal separator which indicates the start of a fractional part, and with a symbol such as the plus sign + (for positive) or minus sign − (for negative) adjacent to the numeral to indicate whether it is greater or less than zero, respectively.

Positional notation uses positions for each power of ten: units, tens, hundreds, thousands, etc. The position of each digit within a number denotes the multiplier (power of ten) multiplied with that digit—each position has a value ten times that of the position to its right. There were at least two presumably independent sources of positional decimal systems in ancient civilization: the Chinese counting rod system and the Hindu-Arabic numeral system (the latter descended from Brahmi numerals).

Ten is the number which is the count of fingers and thumbs on both hands (or toes on the feet). The English word digit as well as its translation in many languages is also the anatomical term for fingers and toes. In English, decimal (decimus < Lat.) means tenth, decimate means reduce by a tenth, and denary (denarius < Lat.) means the unit of ten.

The symbols for the digits in common use around the globe today are called Arabic numerals by Europeans and Indian numerals by Arabs, the two groups' terms both referring to the culture from which they learned the system. However, the symbols used in different areas are not identical; for instance, Western Arabic numerals (from which the European numerals are derived) differ from the forms used by other Arab cultures.

Decimal fractions

A decimal fraction is a fraction whose denominator is a power of ten.

Decimal fractions are commonly expressed without a denominator, the decimal separator being inserted into the numerator (with leading zeros added if needed) at the position from the right corresponding to the power of ten of the denominator; e.g., 8/10, 83/100, 83/1000, and 8/10000 are expressed as 0.8, 0.83, 0.083, and 0.0008. In English-speaking, some Latin American and many Asian countries, a period (.) or raised period (·) is used as the decimal separator; in many other countries, particularly in Europe, a comma is used.

The integer part, or integral part of a decimal number is the part to the left of the decimal separator. (See also truncation.) The part from the decimal separator to the right is the fractional part. It is usual for a decimal number that consists only of a fractional part, (mathematically, a proper fraction), to have a leading zero in its notation (its numeral). This helps disambiguation between a decimal sign and other punctuation, and especially when the negative number sign is indicated, it helps visualize the sign of the numeral as a whole.

Trailing zeros after the decimal point are not necessary, although in science, engineering and statistics they can be retained to indicate a required precision or to show a level of confidence in the accuracy of the number: Although 0.080 and 0.08 are numerically equal, in engineering 0.080 suggests a measurement with an error of up to one part in two thousand (±0.0005), while 0.08 suggests a measurement with an error of up to one in two hundred (see significant figures).

Other rational numbers

Any rational number with a denominator whose only prime factors are 2 and/or 5 may be precisely expressed as a decimal fraction and has a finite decimal expansion.

1/2 = 0.5

1/20 = 0.05

1/5 = 0.2

1/50 = 0.02

1/4 = 0.25

1/40 = 0.025

1/25 = 0.04

1/8 = 0.125

1/125= 0.008

1/10 = 0.1

If the rational number's denominator has any prime factors other than 2 or 5, it cannot be expressed as a finite decimal fraction, and has a unique eventually repeating infinite decimal expansion.

1/3 = 0.333333… (with 3 repeating)

1/9 = 0.111111… (with 1 repeating)

100-1=99=9×11

1/11 = 0.090909… (with 09 repeating)

1000-1=9×111=27×37

1/27 = 0.037037037…

1/37 = 0.027027027…

1/111 = 0 .009009009…

also:

1/81= 0.012345679012… (with 012345679 repeating)

That a rational number must have a finite or recurring decimal expansion can be seen to be a consequence of the long division algorithm, in that there are only q-1 possible nonzero remainders on division by q, so that the recurring pattern will have a period less than q. For instance, to find 3/7 by long division:

     0.4 2 8 5 7 1 4 ...
 7 ) 3.0 0 0 0 0 0 0 0
     2 8                         30/7 = 4 r 2
       2 0
       1 4                       20/7 = 2 r 6
         6 0
         5 6                     60/7 = 8 r 4
           4 0
           3 5                   40/7 = 5 r 5
             5 0
             4 9                 50/7 = 7 r 1
               1 0
                 7               10/7 = 1 r 3
                 3 0
                 2 8             30/7 = 4 r 2
                   2 0
                        etc.

The converse to this observation is that every recurring decimal represents a rational number p/q. This is a consequence of the fact that the recurring part of a decimal representation is, in fact, an infinite geometric series which will sum to a rational number. For instance,

Real numbers

Further information: Decimal representation

Every real number has a (possibly infinite) decimal representation; i.e., it can be written as

where

• sign() is the sign function, and
• a_i ∈ { 0,1,…,9 } for all i ∈ Z are its decimal digits, equal to zero for all i greater than some number (that number being the common logarithm of |x|).

Such a sum converges as i increases, even if there are infinitely many non-zero a_i.

Rational numbers (e.g., p/q) with prime factors in the denominator other than 2 and 5 (when reduced to simplest terms) have a unique recurring decimal representation.

Non-uniqueness of decimal representation

Consider those rational numbers which have only the factors 2 and 5 in the denominator, i.e., which can be written as p/(2^a5^b). In this case there is a terminating decimal representation. For instance, 1/1 = 1, 1/2 = 0.5, 3/5 = 0.6, 3/25 = 0.12 and 1306/1250 = 1.0448. Such numbers are the only real numbers which do not have a unique decimal representation, as they can also be written as a representation that has a recurring 9, for instance 1 = 0.99999…, 1/2 = 0.499999…, etc. The number 0 = 0/1 is special in that it has no representation with recurring 9.

This leaves the irrational numbers. They also have unique infinite decimal representations, and can be characterised as the numbers whose decimal representations neither terminate nor recur.

So in general the decimal representation is unique, if one excludes representations that end in a recurring 9.

The same trichotomy holds for other base-n positional numeral systems:

• Terminating representation: rational where the denominator divides some n^k
• Recurring representation: other rational
• Non-terminating, non-recurring representation: irrational

A version of this even holds for irrational-base numeration systems, such as golden mean base representation.

Decimal computation

Decimal computation was/is carried out in ancient times in many ways, typically in Rod calculus, on sand tables or with a variety of abaci.

Modern computer hardware and software systems commonly use a binary representation internally (although many early computers, such as the ENIAC or the IBM 650, used decimal representation internally). For external use by computer specialists, this binary representation is sometimes presented in the related octal or hexadecimal systems.

For most purposes, however, binary values are converted to or from the equivalent decimal values for presentation to or input from humans; computer programs express literals in decimal by default. (123.1, for example, is written as such in a computer program, even though many computer languages are unable to encode that number precisely.)

Both computer hardware and software also use internal representations which are effectively decimal for storing decimal values and doing arithmetic. Often this arithmetic is done on data which are encoded using some variant of binary-coded decimal, especially in database implementations, but there are other decimal representations in use (such as in the new IEEE 754 Standard for Floating-Point Arithmetic).

Decimal arithmetic is used in computers so that decimal fractional results can be computed exactly, which is not possible using a binary fractional representation. This is often important for financial and other calculations.

History

Many ancient cultures calculated from early on with numerals based on ten: Egyptian hieroglyphs, in evidence since around 3000 BC, used a purely decimal system, just as the Cretan hieroglyphs (ca. 1625−1500 BC) of the Minoans whose numerals are closely based on the Egyptian model. The decimal system was handed down to the consecutive Bronze Age cultures of Greece, including Linear A (ca. 18th century BC−1450 BC) and Linear B (ca. 1375−1200 BC) — the number system of classical Greece also used powers of ten, including, like the Roman numerals did, an intermediate base of 5. Notably, the polymath Archimedes (c. 287–212 BC) invented a decimal positional system in his Sand Reckoner which was based on 10⁸ and later led the German mathematician Carl Friedrich Gauss to lament what heights science would have already reached in his days if Archimedes had fully realized the potential of his ingenious discovery. The Hittites hieroglyphs (since 15th century BC), just like the Egyptian and early numerals in Greece, was strictly decimal.

The Egyptian hieratic numerals, the Greek alphabet numerals, the Roman numerals, the Chinese numerals and early Indian Brahmi numerals are all non-positional decimal systems, and required large numbers of symbols. For instance, Egyptian numerals used different symbols for 10, 20, through 90, 100, 200, through 900, 1000, 2000, 3000, 4000, to 10,000.

History of decimal fractions

counting rod decimal fraction 1/7

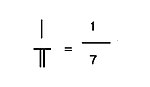
According to Joseph Needham, decimal fractions were first developed and used by the Chinese in the 1st century BC, and then spread to the Middle East and from there to Europe.The written Chinese decimal fractions were non-positional. However, counting rod fractions were positional.

Qin Jiushao in his book Mathematical Treatise in Nine Sections (1247) denoted 0.96644 by

寸

, meaning

寸

096644

The Jewish mathematician Immanuel Bonfils invented decimal fractions around 1350, anticipating Simon Stevin, but did not develop any notation to represent them.

The Persian mathematician Jamshīd al-Kāshī claimed to have discovered decimal fractions himself in the 15th century, though J. Lennart Berggren notes that positional decimal fractions were used five centuries before him by Arab mathematician Abu'l-Hasan al-Uqlidisi as early as the 10th century.

Khwarizmi introduced fractions to Islamic countries in the early 9th century. . This form of fraction with the numerator on top and the denominator on the bottom, without a horizontal bar, was also used in the 10th century by Abu'l-Hasan al-Uqlidisi and again in the 15th century work "Arithmetic Key" by Jamshīd al-Kāshī.^{[citation needed]}

A forerunner of modern European decimal notation was introduced by Simon Stevin in the 16th century.

Natural languages

Telugu language uses a straightforward decimal system. Other Dravidian languages such as Tamil and Malayalam have replaced the number nine tondu with 'onpattu' ("one to ten") during the early Middle Ages, while Telugu preserved the number nine as tommidi.

The Hungarian language also uses a strightforward decimal system. Unlike many indo-european languages, there is no exception between 10 and 20 (e.g. 11 is expressed as "tízenegy" litterarly "one on ten") or between 20-100 (23 as "huszonhárom" = "three on twenty") and the ones never precede the tens (like in german, e.g. "dreiundzwanzig" = 23).

A straightforward decimal rank system with a word for each order 10十,100百,1000千,10000万, and in which 11 is expressed as ten-one and 23 as two-ten-three, and 89345 is expressed as 8 (ten thousands) 万9 (thousand) 千3 (hundred) 百4 (tens) 十 5 is found in Chinese languages, and in Vietnamese with a few irregularities. Japanese, Korean, and Thai have imported the Chinese decimal system. Many other languages with a decimal system have special words for the numbers between 10 and 20, and decades. For example in English 11 is "eleven" not "ten-one".

Incan languages such as Quechua and Aymara have an almost straightforward decimal system, in which 11 is expressed as ten with one and 23 as two-ten with three.

Some psychologists suggest irregularities of the English names of numerals may hinder children's counting ability.