Steinhaus–Johnson–Trotter Algorithm

The Hamiltonian path in the Cayley graph of the symmetric group generated by the Steinhaus–Johnson–Trotter algorithm

The Steinhaus–Johnson–Trotter algorithm or Johnson–Trotter algorithm, also called plain changes, is an algorithm named after Hugo Steinhaus, Selmer M. Johnson and Hale F. Trotter that generates all of the permutations of n elements. Each permutation in the sequence that it generates differs from the previous permutation by swapping two adjacent elements of the sequence. Equivalently, this algorithm finds a Hamiltonian path in the permutohedron.

This method was known already to 17th-century English change ringers, and Sedgewick (1977) calls it "perhaps the most prominent permutation enumeration algorithm". As well as being simple and computationally efficient, it has the advantage that subsequent computations on the permutations that it generates may be sped up because of the fact that these permutations are so similar to each other.

Recursive structure

The sequence of permutations for a given number n can be formed from the sequence of permutations for n − 1 by placing the number n into each possible position in each of the shorter permutations. When the permutation on n − 1 items is an even permutation (as is true for the first, third, etc., permutations in the sequence) then the number n is placed in all possible positions in descending order, from n down to 1; when the permutation on n − 1 items is odd, the number n is placed in all the possible positions in ascending order.

Thus, from the single permutation on one element,

1

one may place the number 2 in each possible position in descending order to form a list of two permutations on two elements,

1 2

2 1

Then, one may place the number 3 in each of three different positions for these three permutations, in descending order for the first permutation 1 2, and then in ascending order for the permutation 2 1:

1 2 3

1 3 2

3 1 2

3 2 1

2 3 1

2 1 3

At the next level of recursion, the number 4 would be placed in descending order into 1 2 3, in ascending order into 1 3 2, in descending order into 3 1 2, etc. The same placement pattern, alternating between descending and ascending placements of n, applies for any larger value of n. In this way, each permutation differs from the previous one either by the single-position-at-a-time motion of n, or by a change of two smaller numbers inherited from the previous sequence of shorter permutations. In either case this difference is just the transposition of two adjacent elements. When n > 1 the first and final elements of the sequence, also, differ in only two adjacent elements (the positions of the numbers 1 and 2), as may be shown by induction.

Although this sequence may be generated by a recursive algorithm that constructs the sequence of smaller permutations and then performs all possible insertions of the largest number into the recursively-generated sequence, the actual Steinhaus–Johnson–Trotter algorithm avoids recursion, instead computing the same sequence of permutations by an iterative method.

Algorithm

As described by Johnson (1963), the algorithm for generating the next permutation from a given permutation π is particularly simple:

• For each i from 1 to n, let x_i be the position where the value i is placed in permutation π. If the order of the numbers from 1 to i − 1 in permutation π defines an even permutation, let y_i = x_i − 1; otherwise, let y_i = x_i + 1.
• Find the largest number i for which y_i defines a valid position in permutation π that contains a number smaller than i. Swap the values in positions x_i and y_i.

When no number i can be found meeting the conditions of the second step of the algorithm, the algorithm has reached the final permutation of the sequence and terminates. This procedure may be implemented in O(n) time per permutation.

Trotter (1962) gives an alternative implementation of an iterative algorithm for the same sequence, in uncommented pseudocode.

Because this method generates permutations that alternate between being even and odd, it may easily be modified to generate only the even permutations or only the odd permutations: to generate the next permutation of the same parity from a given permutation, simply apply the same procedure twice.

Even's speedup

A subsequent improvement by Shimon Even provides an improvement to the running time of the algorithm by storing additional information for each element in the permutation: its position, and a direction (positive, negative, or zero) in which it is currently moving (essentially, this is the same information computed using the parity of the permutation in Johnson's version of the algorithm). Initially, the direction of the number 1 is zero, and all other elements have a negative direction:

1 −2 −3

At each step, the algorithm finds the largest element with a nonzero direction, and swaps it in the indicated direction:

1 −3 −2

If this causes the chosen element to reach the first or last position within the permutation, or if the next element in the same direction is larger than the chosen element, the direction of the chosen element is set to zero:

3 1 −2

After each step, all elements greater than the chosen element have their directions set to positive or negative, according to whether they are concentrated at the start or the end of the permutation respectively. Thus, in this example, when the number 2 moves, the number 3 becomes marked with a direction again:

+3 2 1

The remaining two steps of the algorithm for n = 3 are:

2 +3 1

2 1 3

When all numbers become unmarked, the algorithm terminates.

This algorithm takes time O(i) for every step in which the largest number to move is n − i + 1. Thus, the swaps involving the number n take only constant time; since these swaps account for all but a 1/n fraction of all of the swaps performed by the algorithm, the average time per permutation generated is also constant, even though a small number of permutations will take a larger amount of time.

A more complex loopless version of the same procedure allows it to be performed in constant time per permutation in every case; however, the modifications needed to eliminate loops from the procedure make it slower in practice.

There is a Java implementation of a generic iterator that generates all swap moves required to generate the full set of permutations, using this algorithm. This implementation can be found here.

The algorithm defines a Hamiltonian path in a Cayley graph of the symmetric group. The inverse permutations define a path in the permutohedron:
Cayley graph	Permutohedron
Permutations form a Gray code. The swapped elements are always adjacent.	Permutations, inversion vectors and inversion sets form a Gray code.
Permutations with green or orange background are odd. The smaller numbers below the permutations are the inversion vectors. Red marks indicate swapped elements. Compare list in natural order.

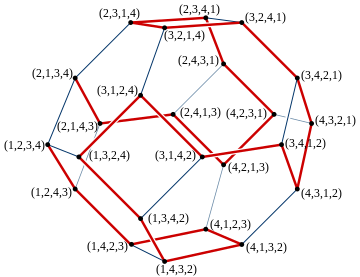
Geometric interpretation

The set of all permutations of n items may be represented geometrically by a permutohedron, the polytope formed from the convex hull of n! vectors, the permutations of the vector (1,2,...n). Although defined in this way in n-dimensional space, it is actually an (n − 1)-dimensional polytope; for example, the permutohedron on four items is a three-dimensional polyhedron, the truncated octahedron. If each vertex of the permutohedron is labeled by the inverse permutation to the permutation defined by its vertex coordinates, the resulting labeling describes a Cayley graph of the symmetric group of permutations on n items, as generated by the permutations that swap adjacent pairs of items. Thus, each two consecutive permutations in the sequence generated by the Steinhaus–Johnson–Trotter algorithm correspond in this way to two vertices that form the endpoints of an edge in the permutohedron, and the whole sequence of permutations describes a Hamiltonian path in the permutohedron, a path that passes through each vertex exactly once. If the sequence of permutations is completed by adding one more edge from the last permutation to the first one in the sequence, the result is instead a Hamiltonian cycle.

Relation to Gray codes

A Gray code for numbers in a given radix is a sequence that contains each number up to a given limit exactly once, in such a way that each pair of consecutive numbers differs by one in a single digit. The n! permutations of the n numbers from 1 to n may be placed in one-to-one correspondence with the n! numbers from 0 to n! − 1 by pairing each permutation with the sequence of numbers c_i that count the number of positions in the permutation that are to the right of value i and that contain a value less than i (that is, the number of inversions for which i is the larger of the two inverted values), and then interpreting these sequences as numbers in the factorial number system, that is, the mixed radix system with radix sequence (1,2,3,4,...). For instance, the permutation (3,1,4,5,2) would give the values c₁ = 0, c₂ = 0, c₃ = 2, c₄ = 1, and c₅ = 1. The sequence of these values, (0,0,2,1,1), gives the number

0 × 0! + 0 × 1! + 2 × 2! + 1 × 3! + 1 × 4! = 34.

Consecutive permutations in the sequence generated by the Steinhaus–Johnson–Trotter algorithm have numbers of inversions that differ by one, forming a Gray code for the factorial number system.

More generally, combinatorial algorithms researchers have defined a Gray code for a set of combinatorial objects to be an ordering for the objects in which each two consecutive objects differ in the minimal possible way. In this generalized sense, the Steinhaus–Johnson–Trotter algorithm generates a Gray code for the permutations themselves.

History

The algorithm is named after Hugo Steinhaus, Selmer M. Johnson and Hale F. Trotter. Johnson and Trotter discovered the algorithm independently of each other in the early 1960s. A book by Steinhaus, originally published in 1958 and translated into English in 1963, describes a related puzzle of generating all permutations by a system of particles, each moving at constant speed along a line and swapping positions when one particle overtakes another. No solution is possible for n > 3, because the number of swaps is far fewer than the number of permutations, but the Steinhaus–Johnson–Trotter algorithm describes the motion of particles with non-constant speeds that generate all permutations.

Outside of mathematics, the same method was known for much longer as a method for change ringing of church bells: it gives a procedure by which a set of bells can be rung through all possible permutations, changing the order of only two bells per change. These so-called "plain changes" were recorded as early as 1621 for four bells, and a 1677 book by Fabian Stedman lists the solutions for up to six bells. More recently, change ringers have abided by a rule that no bell may stay in the same position for three consecutive permutations; this rule is violated by the plain changes, so other strategies that swap multiple bells per change have been devised.